Inside Spacewar!
Part 7: Shootout at El Cassiopeia
(Introduction · Shootout: Torpedoes · The Winds of Space · Now Go Bang: Explosions · Spacewar 2b and the Crock Explosion)
So far, we've covered all kinds of things in our software archeological journey through Spacewar!, like, how to put a lovely moving star-map onto the screen, or even a pulsing heavy star, how to draw little spaceships by compiling configureable outlines, how to move them over the screen, and how to loop over and to handle the objects of this tiny universe, and even, how to pervade this world by gravity — and especially, how to do all this, if no one had ever attempted to do so before. Near all of this was related to space and how to navigate it, but there's still some major part painfully missing, the part related to the war in "Spacewar!". So let's have there some weapons, and maybe even some little pyrotechnics — like torpedoes and explosions.

Space-war as in Spacewar!, joining two eras of space enthusiasm.
Illustration: Norbert Landsteiner, 2014
"[The rockets] were rather crude cartoons. But one of them was curvy like a Buck Rogers 1930s spaceship.
And the other one was very straight and long and thin like a Redstone rocket." — Steve Russell
(quoted from Kent, Steven L. The Ultimate History of Video Games. Roseville, CA: Prima Publishing, 2001).
Let's start with the torpedoes or "mumblemumble photon bombs mumblemumble" (J.M. Graetz, The Origin of Spacewar, Creative Computing, 1981).

Space warfare in Spacewar! (emulation).
BTW: ▶ You can play here the original code of Spacewar! running in an emulation.
Shootout
Spacewar! is essentially a duel in space, or a shootout, as Peter Samson put it when dubbing Spacewar! "Shootout-at-El-Cassiopeia" (Levy, Steven, Hackers, 1984/2010, p.53). — There's some irony in this in more than one sense, since Cassiopeia is actually off to the virtual north of the aspect of the Expensive Planetarium and no one would have known this better than its autor, Peter Samson. (Compare the star-map of the EP in Part 1.) So, with no Cassiopeia in Spacewar!, it would be more like a Shootout-at-High-Orion. — Anyway, no shootout without any weaponry, and the original Spacewar!'s arsenals contained only a single sort of weapon: torpedoes. To be exact, 32 of them for each of the two ships.
Martin Graetz put it more directly in his DECUS paper on Spacewar!, resisting any urge to glorify this as a duel in some past-century sunset: "The object of the game is to destroy the opponent's ship by blasting him out of space with torpedos." (J. M. Graetz, "Spacewar! Real-Time Capability of the PDP-1", DECUS Proceedings 1962, p.37)
And continuing on the more technical aspects of space warfare: "Both ships are armed with ballistic missiles (torpedos) which are released from the nose of the ship with a velocity equal to the ship's velocity plus that imparted to the missile by the launcher. From then on, the torpedos are in true ballistic flight. [...] The torpedos have two types of fuze: one is a proximity fuze which causes the torpedo to explode when it comes within a certain critical distance of any other collidable object which will also be caused to explode. The other is a time fuze which causes the torpedo itself to explode if it has not encountered another object after a given length of time." (ibidem)
We've already seen in Part 5, how the trigger was parsed and how the murderous projectiles were launched: First, the torpedo reload time is checked by a count-up (if, positive, the tubes would be still cooling and we would jump to label sr5 to check the hyperspace trigger). Then, the control input is checked for the third bit from the left being set. If so, we're checking the remaining torpedoes, and if there are any left, we'll search for an unused slot in the objects table. If all went well, a jump takes us to label sr2 for the actual setup.
The Torpedo Code
Spacewar! was conceived in 1961 by Martin Graetz, Stephen Russell, and Wayne Wiitanen. It was first realized on the PDP-1 in 1962 by Stephen Russell, Peter Samson, Dan Edwards, and Martin Graetz, together with Alan Kotok, Steve Piner, and Robert A Saunders. Spacewar! is in the public domain, but this credit paragraph must accompany all distributed versions of the program.
tno, 6, law i 41 / number of torps + 1 tvl, 7, sar 4s / torpedo velocity rlt, 10, law i 20 / torpedo reload time tlf, 11, law i 140 / torpedo life ... the, 21, sar 9s / amount of torpedo space warpage ... define count A,B isp A jmp B term define dispt A,Y,B repeat 6, B=B+B lio Y dpy-A+B term define diff V,S,SF add i V dac i V xct SF add i S dac i S term ... sr2, lac (tcr / set up torpedo calc dac i sr1 law nob add sr1 dap ss3 lio \stx ss3, dio . add (nob dap ss4 lio \sty ss4, dio . add (nob dap sr6 add (nob dap sr7 add (nob dap sr3 add (nob dap sr4 lac \sn xct tvl cma add i \mdx sr3, dac . lac \cs xct tvl add i \mdy sr4, dac . xct rlt dac i ma1 / permit torp tubes to cool trf, xct tlf / life of torpedo sr6, dac . law 20 sr7, dap . / length of torp calc. ... / torpedo calc routine tcr, dap trc count i ma1, tc1 lac (mex 400000 dac i ml1 law i 2 dac i ma1 jmp trc tc1, lac i mx1 sar 9s xct the diff \mdy, my1, (sar 3s sar 9s xct the diff \mdx, mx1, (sar 3s dispt i, i my1, 1 trc, jmp .
(Code as in version 3.1. For the basics of PDP-1 instructions and Macro assembler code, please refer to Part 1.)
Setup
To begin with, let's have a look at the torpedo setup at label sr2.
When we arrive here, we have already identified the address of the next free slot in the objects table, currently in the address part of location sr1. We may recall from Part 3, how this table of colliding objects is organized: It's a stack of properties with the properties of a kind lined up for each of the objects followed by the next array of properties. So, the properties of any object are stored in locations separated by a number of addresses that equals the total number of objects as in nob. The locations describing the current object are usually aliased by labeled pointers and addressed indirectly (or deferred) by the use of the i-bit. The code starting at sr2 is setting up a new object by initializing the corresponding properties with suitable values:
(As usual, comments starting with a double slash are mine; N.L.)
sr2, lac (tcr / set up torpedo calc dac i sr1 // store address tcr as the object routine law nob // load number of objects into AC add sr1 // add sr1 (object's base address to it) dap ss3 // store it in ss3 lio \stx // load current x into IO ss3, dio . // store it as torpedo x add (nob // add number of objects (next property) dap ss4 // store it in s4 lio \sty // now set up y ss4, dio . ...
Generally, the code is following the same pattern, we've already seen for the setup of the spaceships, suggesting it was done by the same author, Steve Russell. First, the start address of the torpedo routine tcr is stored as the torpedo's object routine. Since there isn't a set sign-bit (as in "(tcr 400000") the object is collidible and any collisions with other objects will be checked by the main loop. By adding nob to the address of this first property, we advance to the next property, the x-position. This is set up and stored at label ss3. The same procedure is applied for the y-position, set up and stored at label ss4. The position in variables \stx and \sty was already computed in the spaceship routine while setting up the factors for drawing the outline and happens to be just in front of the tip of the firing ship.
add (nob dap sr6 add (nob dap sr7 add (nob dap sr3 add (nob dap sr4 lac \sn // load sine xct tvl // scale it (sar 4s) cma // complement it (reverse the angle) add i \mdx // add current delta x sr3, dac . // store it as torpedo dx lac \cs // same for cosine and dy xct tvl add i \mdy sr4, dac . xct rlt // get torpedo reload time (-20) dac i ma1 / permit torp tubes to cool trf, xct tlf / life of torpedo //(-140) sr6, dac . law 20 sr7, dap . / length of torp calc.
Now, the adresses of the next properties are set up in the address parts of locations sr6, sr7, sr3, and sr4. Time to setup the direction of the torpedo. Obviously we would want it to move in the direction the spaceship is currently heading to, and obviously, we would want it's eigen-velocity to add to the base velocity of the ship. (Otherwise, a fastly moving ship would be prone to overtake it, just to be destroyed by its own torpedo. Not to speak of simulating Newton's laws.) Fortunately we've the sine and cosine of the ship's current turning angle ready in variables \sn and \cs respectively. We just have to scale this unit vector in order to arrive at an appropriate eigen-vector. This scaling is done by "xct tvl", which will execute the instruction "sar 4s", a right-shift by 4 bits (divide by 16). To this we add the current movement of the ship, as in \mdx (delta x) and \mdy (delta y). The resulting quantities are then stored as properties of the torpedo, when executing sr3 (dx) and sr4 (dy) respectively.
Since our torpedo will be just displayed as a tiny dot, there's no need to store a turning angle, since, a dot is a dot is a dot is a dot. (Thank you once more, Gertrude Stein.) So, we've just to deal with the timing issues before we're actually finsihed: There are two different kind of intervals involved (both involving negative values to be used in a count up), the torpedo reload time (or torp tubes cooling) and the life of the torpedo, the number of frames to be passed before it will be destructed by its virtual time fuse.
The first one is loaded by executing "xct rlt". This will execute the instruction "law i 20" (defined in the table of constants at the top of the source, just like tvl), loading the number -20 into the accumulator. The cooling time is actually a property of the firing ship and stored in the address currently in pointer \ma1. The torpedo life is obtained by executing "law i 140" (loading -140) by the instruction "xct tlf" and stored in the according property at label sr6. Finally, the estimated cycle count (20) of the torpedo routine is stored in the last property at label sr7, to be used to stabilize the frame rate.
Thus, we've just initilized a fresh torpedo with the following properties:
addr property value common alias base object routine address tcr ml1 +nob x just in front of the ship mx1 +nob y --"-- my1 +nob dx sine of ship / 16 + ship dx \mdx +nob dy cosine of ship / 16 + ship dy \mdy +nob torpedo life -140 (140 frames) ma1 +nob cycle count 20 (actually decimal 16×4 = 64) mb1
Since the spaceships are occupying the very first two slots of the objects table, our fresh torpedo is located at some higher slot and will be found and handled by the main loop in the same frame by calling its object routine:
Movement
Handling a torpedo involves basically three tasks: Moving it through space (and displaying it), having an eye at the time fuse, and checking any collisions. With the latter one already handled by the main loop, the torpedo routine has just to take care of the two other ones. Just like we've seen it for the spaceships, all the essential properties are already aliased by some pointers, when our object routine is called, with the current object now being the torpedo:
tcr, dap trc // store return address count i ma1, tc1 // check life time lac (mex 400000 // oops, expired - set up an explosion dac i ml1 // store explosion code as the new object routine law i 2 // load -2 dac i ma1 // store it as the new life time jmp trc // return
As usual, our first task is to store the return address (currently in the accumulator), here in the address part of location trc. Next, we increment the life count by calling the macro "count i ma1, tc1" and if still negative, we'll continue at label tc1.
If the increment would result in a positive value, our torpedo expired and its time to "go bang". To set up the explosion, we're loading the address of the explosion code "(mex 400000" (since we're adding a set sign-bit, the exploding torpedo won't collide with any other objects) and store this as the new object routine in the address in pointer ml1 (pointing to the very first property of the torpedo). Since our explosion will be just a short one, -2 is stored as the new life time in ma1 for the benefit of the explosion code. Then, looking farward to watching a neat explosion in the next frame, we'll jump to the return at label trc.
Otherwise, we still have to move and display the torpedo.
As we may recall from Part 6, gravity calculations are an hefty business, taking something in the range of 4800 to 4955 microseconds for a single object. No way, we could do this for each of the torpedoes — thus the "mumblemumble photon bombs". Therefor we could expect the movement routine to be fairly simple, just adding the dx and dy values to the positional vector and putting this location onto the screen. But there's a little extra that is usually going unnoticed with the default settings:
tc1, lac i mx1 // load mx1 (x) sar 9s // shift right 9 bits xct the // apply warpage constant (sar 9s) diff \mdy, my1, (sar 3s // update \mdy (+AC) and my1 (+ \mdy>>3) sar 9s // my1 (y) now in AC, repeat for \mdx, mx1 xct the diff \mdx, mx1, (sar 3s dispt i, i my1, 1 // display a blip trc, jmp .
This is loading the x-position into the accumulator to be scaled by a shift to the right by 9 bits. Then, another scaling is applied to this, executed from location the in the constant table. Finally, the position is updated by the macro diff, which updates the first parameter by adding the contents of the accumulator to it, then scales the updated value by applying the shift in the third parameter, and finally updates the second parameter by adding this:
define diff V,S,SF add i V dac i V xct SF add i S dac i S term
Thus, \mdy (delta y) is summed with the contents of AC and stored, then, after applying a shift to the right by 3 bits (just the same scaling factor as with the spaceships, which makes some sense, since we copied the movement vector from the firing ship), the y-position in my1 is updated and the torpedo actually moved. With the updated value of my1 now in the accumulator, the same procedure is repeated for \mdx and mx1. Finally, the updated position is brought to the screen as a slightly brighter (and larger) than average blip by including the macro disp:
define dispt A,Y,B repeat 6, B=B+B lio Y dpy-A+B term
The pseudo-instruction "repeat 6, B=B+B" is effectively a shift by 6 bits, moving the brightness parameter into the right position to be added to the dpy instruction. Since parameter A is the defer bit i, the display command is a fire and forget, without waiting for the display to send a completion pulse when displaying the dot at the location in AC (x) and IO (y), loaded from the second parameter.
Now, whatever would have been set up in the accumulator before including the macro diff is clearly without effect with the default settings, since shifting this value twice by 9 bits to the right is essentially shifting out any contents of the 18-bit register, whatever it might have been. Thus, with no effect on the torpedo and the bare delta-vector added to the position, the torpedo will move in a straight line.
But, what, if there would be a smaller scaling, something less than, say, "sar 8s"? (Since the maximum value of any screen coordinate is octal 777, half of it is an 8-bit value. Therefor a shift by 8 bits to right would clear the accumulator as well.)
Obviously this is a variation on the ancient art of drawing a circle in incremental steps by shifts (here in pseudo-code):
loop: load y shift right 2 add x store x ; x := x + y / 4 complement AC shift right 2 add y store y ; y := y - x / 4 display x, y jump loop
Note: This algorithm for drawing a circle by additions/subtractions and shifts only was discovered by Marvin Minsky by a mistake that brought an unexpected circle-like ellipse onto the display instead of the expected curve. [Compare HAKMEM "Item 149 (Minsky): Circle Algorithm"] — A discovery that led eventually to the famous Minskytron ("Three-Position Display" by Marvin Minsky). We may observe that this algorithm was brand new, when it found its way into the code of Spacewar!.
By increasing the scaling factor applied by the right-shifts, we would arrive at an increasingly neat circloid. While a divide by 16 would do for a nice cirlce, the shift by 9 bits (a divide by 512, with the extra shift by 3 bits even by 4096) is quite fine in granularity and any additional shifts in "the" would further diminish the effect. The omission of the complementing step isn't an issue here, since we are only dealing with some kind of deviation. (Also, we will never achieve at a full circle by our 140 steps, more like a quadrant at best.)
So, to what kind of effect would this add up?
The Winds of Space
Winds of Space is adding another topological effect to the Spacewar-universe: While there is gravity for the ships, there is "space warpage" for the torpedoes. Adding the scaled inverse position in incremental steps to the position of the torpedoes works out as some sine-like modulation of the trajectories which is depending both on the current position of the torpedo and its velocity (since the same amount of deviation would add up to a smaller effect on a longer movement vector).
This is, how the space is bent for the torpedoes, if no scaling at all is applied in "the" in order to achieve the maximum effect:
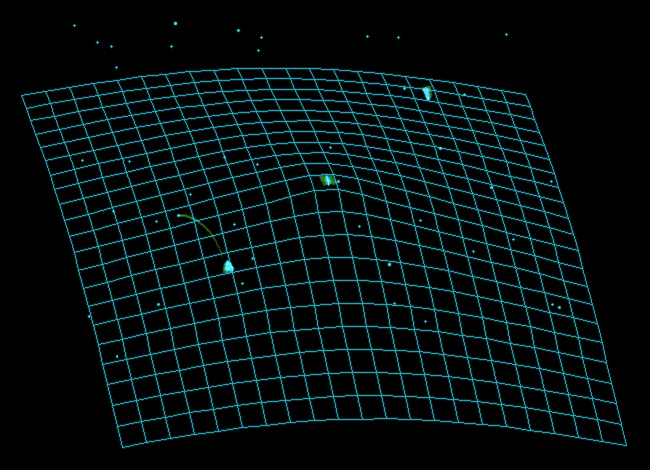
Torpedo space warpage in Spacewar!
(Special purpose emulation, isometric projection, z-axis: strength of effect, orientation downwards, scaling 100:1.)
As we may observe, there's no effect at the center, with the maximum deviation being applied at the edges and corners of the screen. A shot fired from a motionless ship at the start position will produce a rather pathetic arc with the ship firing virtually "uphill", while a torpedo fired from a fast moving ship will result in a trajectory which is bending away quite elegantly from the line to the initial target:
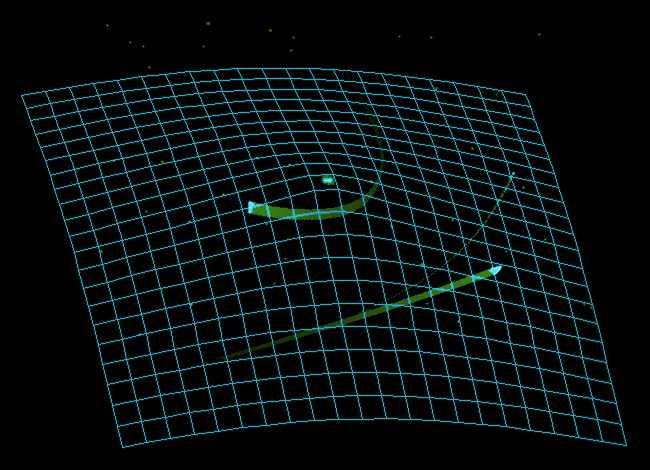
Torpedo space warpage at higher speed.
(Special purpose emulation, isometric projection, z-axis: strength of effect, orientation downwards, scaling 100:1.)
Steven Levy provides an account of the use of Winds of Space as a late night party game to be engaged, when the eyes of the Spacewar-pilots would have become blurry after hours of staring at the luminous screen of the PDP-1's Type 30 CRT (Levy, Steven, Hackers — Heroes of the Computer Revolution; 1984/2010, pp. 51):
The variations were endless. [...] [A]s the night grew later and people became locked into interstellar mode, someone might shout, “Let’s turn on the Winds of Space!” and someone would hack up a warping factor, which would force players to make adjustments every time they moved.
"Hack[ing] up a warping factor" would have involved setting up location 21 in the address switches of the PDP-1's console for the constant "the" (the only warping factor there is), flipping the switches of the test word to set up a small scaling factor and injecting this back into memory by deploying the "deposit" switch. But this wasn't the only effect to be applied by modifying the constants table that even achieved a name, there's another related to torpedoes, too, involving the "torpedo reload time" in constant "rlt" (and possibly some other paramter(s) like the "torpedo velocity" in constant "tvl"):
By switching a few parameters you could turn the game into “hydraulic spacewar,” in which torpedoes flow out in ejaculatory streams instead of one by one. (Levy, Steven, ibidem)
(You may experiment with these constants too, by selecting the item "Hack Parameters..." from the options menu at the top right of the online emulator. There's also a special version for Winds of Space already set up to its maximum effect, to be chosen from the versions menu.)
*****
Note: There are other sources describing the Winds of Space as an effect exerted rather on the spaceships than on the torpedoes: "a 'winds of space' feature could be added which pushed spaceships in one direction, forcing players to use more thrust to go in certain directions and causing drift" («ahoodedfigure», The History and Impact of Spacewar! (1962), 2009 ca., also in Giant Bomb, Spacewar! wiki, as of 19 Apr 2014). — We have to stress here that there are no signs or traces of any other warping factor to be applied in the game (neither in version 2b, nor in version 3.1 or any of the variations of version 4.x) but the one affecting the trajectories of the torpedoes (to be found in version 3.1 and higher). — Another source may serve some further clue by not only attributing Winds of Space to Peter Samson, but also describing it as some prototype feature that would have been eventually dismissed: "More prototypes follow, like Peter's Winds of Space. But adding a constant force that increases as your spaceship moves away from the star, driving the ship perpendicular to its direction of movement, isn't exactly a hit either." (Zarembsky, Ilya, Mother, 2013). While it is quite unclear, what the source for the first of these two passages would have been, the second one seems to be drawn directly from the Q&A session "Spacewar! A Conversation with Steve Russell and Peter Samson", held at the Museum of the Moving Image on 1 Feb 2013. Considering this more closely, it appears to be at least counterintuitive to introduce an antigravitational force to counteract the determinant property of the Spacewar-universe. We might suppose some kind of missinterpretation or an error in recollection here, especially, as there is apparently no transcript of this session. Notably, the torpedo space warpage is also applying a constant force increasing towards the edges that is acting perpendicular to the trajectories of the torpedoes. Also, the Winds of Space seem to be remembered too well to have been just a short-lived, experimental feature. On the other hand we may assume this feature to have existed for a short periode as described here and been migrated to the torpedo code later.
However, there is an account on an other dismissed feature related to torpedoes, provided by Steve Russell in the long version of Stewart Brand's famous Rolling Stone article "Spacewar – Fanatic Life and Symbolic Death Among the Computer Bums" (Rolling Stone, Dec 1972), published in the book "Two Cybernetic Frontiers" (Random House, NY, 1974) by the same author:
One of the things I experimented with was putting a little more realism in it. The torpedoes in Spacewar go plodding along very reliably. I said, "Gee, that's not real. Most real-world devices have some noise in them." So I put a little random error in the torpedoes. They wouldn't always go quite the direction you aimed them, and they didn't always go quite as far as you expected, and they didn't go quite as fast as you expected. I thought it was kind of a neat idea, but everybody just hated it. And if you think about it, you'll see that people take a great deal of effort to make sure that their guns and knives and other offensive weapons are the best they can have. That variation died very quickly. (Steve Russell quoted in "Two Cybernetic Frontiers", p. 56)
Steve Russell's recount not only provides some insight in Spacewar! — as we know it — being a rather distilled and refined version that has undergone a number of probing iterations, but also illustrates the fine line between the realism of a simulation and the rather reduced, reliable set of features contributing to its qualities as a satisfying game.
Now Go Bang!
Fireworks have been always appealing to humans, so how could Spacewar! miss out on the opportunity to put some onto the PDP-1's scope? So, if a ship happens to collide with another object, like the opponents ship or a torpedo, or would be helplessly drawn to a final plunge into the heavy star with sense switch 5 on, we're up for a neat explosion. Actually, there are five kinds of explosions (as we have learned here and in Part 3), a big one resulting from the two ships colliding, a slightly smaller one for a single ship, a tiny one for an expiring torpedo falling prey to its time fuse, and just some short flicker for a torpedo colliding with another one — and finally, a last big one for a ship exploding in the star (see Part 6).
We know from a comment by Steve Russel that Martin Graetz wasn't only the author of the original hyperspace, but also the autor of the explosion routine (MIT TMRC-Talk mailinglist, 31 Jan 2005):
J. M. ("Shag") Graetz contributed the explosions, and Pete Samson wrote the starfield display.
Another (soft) source on this is J.M. Graetz's rather sarcastic description of the explosions in Spacewar! 2b as "crock explosions" (we'll come to those later) in his seminal article "The Origin of Spacewar" (Creative Computing, 1981), a tone he usually reserved for his own contributions only. But we do not know, whether the final adjustments we see in the code of Spacewar! 3.1 were done by him, too, or would have been applied by some other author (Steve Russell?).
The Code
/ explosion mex, dap mxr cla diff \mdx, mx1, (sar 3s cla diff \mdy, my1, (sar 3s law mst dap msh lac i mb1 / time involved cma cli-opr sar 3s dac \mxc ms1, sub (140 sma idx msh mz1, random and (777 ior (scl dac mi1 random scr 9s sir 9s msh, xct . mi1, hlt add i my1 swap add i mx1 dpy-i 300 count \mxc, mz1 count i ma1, mxr dzm i ml1 mxr, jmp . mst, scr 1s scr 3s
Macros used:
define swap rcl 9s rcl 9s term define count A,B isp A jmp B term define dispt A,Y,B repeat 6, B=B+B lio Y dpy-A+B term define diff V,S,SF add i V dac i V xct SF add i S dac i S term define random lac ran rar 1s xor (355670 add (355670 dac ran term
When investigating the explosion routine we must not forget that this is just an object routine. Explosions aren't objects of their own, but these are the normal objects, spaceships and torpedoes, which are now linked to this routine. The objects have still all their properties as in their previous state, aliased by the usual pointers. The only property with a special meaning to an exploding object is the value in the general purpose counter ma1, controlling here the timing of the explosion. Notably, there will be two explosions at once for any collision of two objects.
Inertia
While we're separating the code here into two parts, the code for the explosion is a single strain of code. There's no setup or special coda, the code will be entered at location mex during each frame for each exploding object:
mex, dap mxr cla diff \mdx, mx1, (sar 3s cla diff \mdy, my1, (sar 3s
The explosion routine mex starts with the obligatory storing of the return address (here in the address part of location mxr). The next few instructions are applying the movement vector to the current position, just as we've seen it for the torpedoes before. Thus, conforming with the laws of inertia, an exploding object will keep on moving along its trajectory. Since the accumulator is cleared by the instruction cla before including the macro diff, there's no other factor applied to this movement and the explosion will just keep the direction and velocity of the formerly solid object.
Particles
Before we have a closer look at the code for the animation, we may recall some essential properties of the objects potentially involved here:
Some essential properties of exploding objects and their values (cotal): object colliding with ma1 mb1 (cycle count) ship star -10 2000 ship ship -7 2000 ship torpedo -3 2000 torpedo ship -3 20 torpedo torpedo 1 20 torpedo time fuse -2 20
The first part of the animation code is meant to set up the scaling or spread of the effect. There are essentially two scaling factors, a shift by 1 bit to the right (divide by 2) at label mst and a shift by 3 bits (divide by 3) located immediately following to it. Based on the contents of the property in pointer mb1 (the cycle count) either the address of the single-shift or the address of the triple-shift will be set up in the address part of the xct instruction at label msh:
law mst // load address of instruction "scr 1s" dap msh // deposit it in addr. part of msh lac i mb1 / time involved cma cli-opr // clear IO and compliment AC (now negative) sar 3s // divide it by 8 dac \mxc // store it in \mxc ms1, sub (140 // greater than 140? sma // no, skip idx msh // increment msh, now address of "scr 3s" (never seen) ... msh, xct . ... mst, scr 1s scr 3s
Here is actually a small bug (that never was fixed in any of the subsequent versions of Spacewar!), prohibiting the code from working as intended: What the code is meant to do, is to assign the address of a shift instruction to the location labeled msh, depending on the size of the explosion as derived from the instruction count in pointer mb1. In order to do so, first the address of label mst for a combined single-bit shift to the right ("scr 1s") is set up in the address part of msh. Then the cycle count in property mb1 is loaded and processed: This is a positive number and is first complemented to a negative number to be used in a count up. Then, a shift to the right by 3 bits (a divide by 8) is applied and the result is stored in variable \mxc, giving the number of particles. (For a spaceship with an instruction count of 2000 this will now be -200, for a torpedo of an instruction count of 20 this will be -2.)
The next instructions are comparing this to threshold of octal 140: After subtracting the constant 140, the instruction sma (skip on minus AC) skips, if the result would be negative (\mxc < 140). Otherwise the contents of msh is incremented by the instruction idx and the address part is now pointing to the shift to a combined right-shift by 3 bits ("scr 3s"). — But this instruction will be never visited!
Since \mxc is holding a negative value already, the result of the subtraction will be always negative and the modification of the pointer to the shift instruction ("idx msh") will be always skipped. Thus, the shift will be always "scr 1s". What's missing here, is another cma instruction to revert the contents of AC to a positive number before the comparision is done. However, the resulting explosions are still pretty and we're not missing much.
With the scaling set up in the address part of location msh, we're ready to apply it, to whatever this might be:
mz1, random // put random number in AC and (777 // apply 9s as a mask ior (scl // add opcode scl to it dac mi1 // deposit this instruction in mi1 random // get a new random number scr 9s // split it into AC 9 lower bits and IO 9 lower bits sir 9s msh, xct . // execute shift to the right (AC and IO, either mst or mst+1) mi1, hlt // replaced by random shift to the left (AC and IO)
The macro random (we've seen this before in Part 2 and Part 5) puts a random number into the accumulator (and also stores it in the location ran, which is of no further interest here). This random number is now masked by the and instruction. The following "ior (scl" adds the opcode of the instruction scl to it. Since 777 is the same as the assembler constant 9s, we just assembled an instruction on the fly that will shift both the IO register and the accumulator to the left by something in the range of 0 bits (essentially a void instruction) and the maximum shift of 9 bits. This instruction is then inserted at label mi1.
By including the macro random once more, we get a fresh random number that is then split to the lower halves of the accumulator and the IO register. This is achieved by first shifting the combined registers right by 9 bits and then shifting the former lower half of the random number, now in the higher 9 bits of IO, by another 9 bits to the right. Currently, the two registers are containing some values in the range of -377 .. +377 and both are of the same sign.
Now we're finally applying our carefully prepared shift instructions: The first one will be executed by the xct instruction at label msh. As we've seen above, this was meant to exute either the instruction at label mst or the next instruction following to it, dependending on the cycle count in property mb1, thus applying either a shift to the right by 1 bit to AC and IO as a combined 36-bit register or a shift by 3 bits. Effectively, we inserted the address of location msh in the address part of the xct instruction in any case and therefor we'll execute a right-shift by single bit. (This shift — by whatever number of bit-positions — is not only a division: since scr applies a shift to AC and IO as a combined register, this may have some crucial effect on the contents of IO, notably by shifting in a new sign bit. In rare cases, where this bit isn't shifted out again in the next step, we'll see some artifacts for IO is then converted to a quite high value, resulting in a considerable offset on the effective x-position of the following display instruction.) The next instruction at label mi1 is an entirely random shift to the left that we've just assembled and injected here previously. Notably, this is the shift that will move any bits in the two registers into the range of the highest 10 bits that is used for any display coordinates.
add i my1 // add y swap // swap AC and IO add i mx1 // add x dpy-i 300 // display it at brightness 3 count \mxc, mz1 // count up on \mxc, jump to mz1 while negative count i ma1, mxr // increment ma1, jump to mxr, while negative dzm i ml1 // over, remove object mxr, jmp . // return
By adding the y-coordinate of the object to the accumulator, we get the effective display coordinate for our blip. The macro swap (see Part 2) exchanges the contents of the IO register and the accumulator (by applying "rcl 9s" twice), making this the y-parameter of the display command. After adding the x-coordinate (in property mx1), we are finally ready to bring something onto the screen: The instruction "dpy-i 300" displays a dot at the given coordinates at the highest available intensity of 3 (provided in the third lowest nibble).
But this was not the only blip to be displayed, the count up on variable \mxc (the one we prepared near the entrance of the routine), repeats this sequence by a jump to label mz1 (the first inclusion of the macro random) until the value would have become zero (and thus positive).
The final count increments the contents of property ma1. If still negative, we jump to the return at label mxr. Otherwise we're done and the instruction "dzm i ml1" resets the control word in property ml1 to zero, thus effectively removing the object from the display list. (Since ma1 was pointing to a memory register that contained 1 for a torpedo colliding with another one, this will be the shortest of all explosions, to be displayed just in a single frame. Due to the afterglow of the P7-phosphor of the Type 30 CRT, this will be still visible as a fading flick on the scope.)
We may now complete our table describing the various types of explosions (all values octal):
object colliding with ma1 mb1 particles scr scr frames
(intended) (effective)
ship star -10 2000 200 3s 1s 10
ship ship -7 2000 200 3s 1s 7
ship torpedo -3 2000 200 3s 1s 3
torpedo ship -3 20 2 1s 1s 3
torpedo torpedo 1 20 2 1s 1s 1
torpedo time fuse -2 20 2 1s 1s 2
While the routine isn't exactly about a particle animation as in particle physics, it puts a nice cloud of flashing pixel dust on the Type 30's screen, where it will fade slowly away due to the P7-phosphor's long sustain. The stronger scaling applied to bigger explosion might be counter-intuitive at first sight, but it provides for a high-density center for an exploding solid object with just enough chance left for some stray particles reaching out into space.
Generally the algorithm is producing a random deviation to be added to the object's position for each of the particles, and it seems to do so symmetrically along the two axes. But there is more to it. It's true for the value in the accumulator, destined to become the offset along the y-axis, that there is a scaling applied to limit the amount of the deviation and that there's another random scaling to the left producing the visible offset. But it's a different affair for the value in IO, ultimately becoming the x-offset: Since the two shift instructions (scr and scl) are not only a shift on both of the two registers, but on the two registers as a combined one, the shifts instructions will put a random bit in the sign-position and by this will also convert a previously small number into a big one (as any leading zeros are becoming ones in 1's complement). Moreover, a shift to the right by 3 bits may also put something into the next two highest bits, depending on the contents and sign in AC. Therefor, especially true for an exploding ship, the horizontal spread will be a utterly random one and will not be confined by the first scaling shift to the right. Occasionally, it may also produce some artifacts in the form of stray pixels displayed at some location off to either side, if this would coincide with a rather high random shift to left.
(We will see below that there was even an attempt made to get rid of these artifacts by changing the value of the modifier constant in the macro random from 335671 to 355670 with the lowest 3 bits set to zero. But since there is always a new bit shifted in from the left — and in the absence of any other masking operation, like applying an AND —, this is essentially without effect. Moreover, the lowest nibble is in that part of the of the random number that will be moved into IO and won't matter anyway.)
And there is yet a last issue, as an attentive reader might have observed already: While the original estimated cycle count in mb1 is used to determine the size of the object and hence of the explosion, there are no means to adjust the runtime for the time spent in the explosion routine. Will there be any difference? Since the explosion routine isn't that long, we can do the math: For a spaceship, there are about 43 CPU cycles spent in the animation loop for each of the 128 (octal 200) particles, making a total of 5504 cycles, plus another 50 one in front and after the loop. Thus, we arrive at a sum of decimal 5554 (octal 12662) CPU cycles spent over the entire routine. Since any extra cycles are spent in a loop consuming 4 cycles, we'll have to divide this by 4 in order to arrive at an equivalent of a mb1-cycle-estimate of octal 2554. Since the base value for a spaceship is octal 2000 and the explosion is rather short, there won't be much of a difference to be perceived by the players. Chances are, the players would be rather caught by the attractive effect on the scope than distracted by a small delay for a fraction of a second, if there would be any at all. (We haven't done the math on the standard spaceship routine for comparison, rather relying on the estimated cycle count. But we might be confident that it would yield a rather similar result.)
Spacewar 2b and the Crock Explosion
The code we've just inspected wasn't the originally one. Before, there was the boxy "crock explosion" of Spacewar 2b. Martin Graetz gives a rather sarcastical description in his account of how Spacewar! came into being (J.M. Graetz, The Origin of Spacewar, Creative Computing, 1981):
It's hardly surprising, then, that we had to let a few unsatisfactory (all right, inelegant) bits go by.
The most irritating of these (and the first to be improved in later versions) was the appropriately-named Crock Explosion. Something dramatic obviously had to happen when a ship was destroyed, but we were dealing with a plain dot-matrix screen. The original control program produced a random-dot burst confined within a small square whose outlines were all too discernible (Figure 5).
This explosion was intended merely as a place-holder until something more plausible could be worked out, but after all the other features had been "inhaled," there wasn't room or time for a fancier calculation.
And here is Figure 5, showing the self-accusingly dubbed "crock explosion":
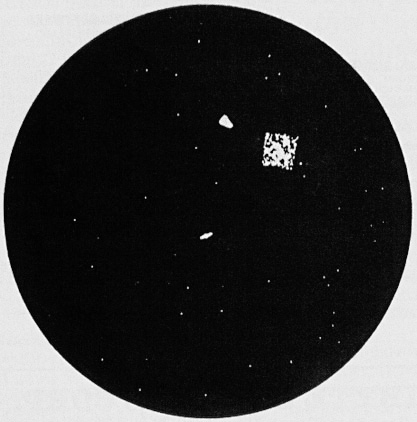
Origin of Spacewar, Figure 5.
Image credits: J. M. Graetz, 1962/1981
Original caption: The Crock Explosion. Nobody's perfect.
And here, for comparison, is the explosion as rendered by Spacewar! 3.1:

Spacewar 3.1: Two ships exploding in a collision (emulation).
Note: Peter Samson's TMRC Dictionary 1st Ed. (June, 1959) helpfully provides a definition of the term "crock" as used in a MIT-related environment: "1) something which fails the purpose of its design from the moment of its conception on; 2) something which by normal or accelerated decay is utterly worthless; 3) (by acrophony) a Coca-Cola."
(Let's put it this way, no, we're not facing a can bottle of Coke, but "accelerated decay" might actually be involved in the thermodynamics of an explosion …)
So, what went wrong, and, how has this been fixed without adding much of a "fancier calculation" that would overburden the tightened ressources of "room and time"?
Let's have a look at the diff of Spacewar 3.1 and Spacewar 2b (this being the original source that has been rediscovered recently):
Spacewar 3.1 24 Sep 62 Spacewar 2b 25 Mar 62
define define
random random N
lac ran lac N
rar 1s rar 1s
xor (355670 xor (335671
add (355670 add (335671
dac ran dac N
term term
... ...
/ explosion / crock explosion
mex, dap mxr mex, dap mxr
cla cla
diff \mdx, mx1, (sar 3s diff \mdx, mx1, (sar 3s
cla cla
diff \mdy, my1, (sar 3s diff \mdy, my1, (sar 3s
law mst law mst
dap msh dap msh
lac i mb1 / time involved lac i mb1 / time involved
cma cli-opr cma cli-opr
sar 3s sar 2s
dac \mxc dac \mxc
ms1, sub (140 ms1, sub (500
sma sma
idx msh idx msh
mz1, random mz1, random \ran
and (777
ior (scl
dac mi1
random
scr 9s scr 9s
sir 9s sir 9s
msh, xct . msh, xct .
mi1, hlt
add i my1 add i my1
swap swap
add i mx1 add i mx1
dpy-i 300 dpy-i
count \mxc, mz1 count \mxc, mz1
count i ma1, mxr count i ma1, mxr
dzm i ml1 dzm i ml1
mxr, jmp . mxr, jmp .
mst, scr 1s mst, scl 5s
scr 3s scl 2s
First of all, we may notice the self-accusing term "crock explosion" being even in the source, a manifest of the merely assuaged pains of its developer. (Although, as for the aesthetic side of things, it worked out quite nicely together with the Minskytron-effect of the original hyperspace routine. — It is quite interesting that, if we replace the explosion routine of Spacewar! 2b by the one of version 3.1, there's something missing. The two effects do not go together that well. This might be one of the reasons, why the warp-induced photonic stress emission hyperspace signature was ulimately dismissed, with a priority on the explosions.)
Second, there isn't that much change, only a mere 5 instructions were added and the values of a few constants were modified. (Also, in Spacewar! 2b, the random number generator isn't working on a fixed, labeled memory location for the random number to be stored in, but is rather fed with the variable \ran as a parameter. But this isn't making much of a difference.)
So, what's different? First, the number of particles is reduced to the half by applying a shift by 3 bits to the right to the contents of property mb1 rather than a shift by 2 bits. For this, the comparision to the constant 500 to identify the big ones, is also reduced to 140. (Again, this comparison is ineffective for the same reasons we've observed obove. Thus, a shif by 5 bits, see below, will be used in any case.) Second, and more importantly, the shifts for the confining box are reduced and the additional random shift to the left at label mi1 has been added, as well as the 4 instructions for setting it up. (We may observe in Spacewar! 2b that the scaling shift at mst is a shift to the left and that it is intended to be a greater one for the smaller explosions than for the bigger ones.) Moreover, the not so perfect symmetry provided by the various shifts applied to the x- and y-deplacements adds to a more "natural" spread of the particles in Spacewar! 3.1.
Putting it the other way round, what went wrong in Spacewar! 2b?
Let's have a look: Like in Spacewar! 3.1, there's a random number split into two halves, each of them in the lower bits of IO and AC in the range of -377 .. +377, when we arrive at label msh to execute the scaling shift. Since the resulting value will be added to a screen coordinate (to be considered as a frational value with the fractional point placed after the 10th bit from the left), only the highest 10 bits will be of interest here. With 377 equaling all of the 8 lowest bits set, the shifts will produce a visible effect only for the amount of bit positions the contents is moved, at best. Thus, the left-shift by 5 bit positions effects in a maximum displacement of decimal 31 screen locations in any direction (or 32 locations with the inclusion of a possible carry). Moreover, the original algorithm is producing a perfectly symmetrical result along the two axes, since this is a shift to the left with the higher part of the two registers cleared. Since there are also twice as many particles (e.g., octal 400 for a big explosion), we meet a fair chance to see the confining box filled by a random pattern.
Another difference is not to be found in the explosion routine itself, but in the macro random for the random number generator. Here, there's this change to the modifier constant, we've alread addressed above. Since the random number is else used for the display of the central heavy star and for the random length of the exhaust blasts — and both of them remained essentially unchanged —, we may conclude that this was done to address an issue with the explosions, namely the occasional stray particles produced by the modified animation algorithm. This might also provide a clue about the authorship of the modifications we see in version 3.1: Both the straight forward style of this intervention and the change of the RNG modifier may hint at Steve Russell. — At least: Who else would have dared to mess around with the random number generator? (Opposed to this, we do not see the use of a hlt instruction as a placeholder anywere in the code that might be attributed to Steve Russell with some certainty.)
*****
While speaking of Spacewar! 2b, this might also be the place to note some of the major changes applied to the game in version 3.1: Generally, Spacewar! 3.1 appears to be a consolidated version of Spacewar! 2b, with most of the code unchanged, but with the various patches now integrated into the main source. Prominent changes are the start position of the EP and the introduction of modulated display intensities, a new hyperspace routine, the double length rocket blasts, and the changes to the explosion routine, we've investigated here. But there are also some other changes under the hood, namely the extraction of some modifier constants and their integration in a common table on top of the program to be easily accessed by the operator's console. Moreover, some of these values were adjusted in favor for a more fluent and a bit faster game. We don't know, if the introduction of the constants table would have been motivated by the need to rework these values, or if the refined values would have been rather a result of the experiments made on them. Anyway, we may observe some shift in emphasis, from Spacewar! representing a simulation towards an emphasis on the play value of the program as a game. — A slight shift in perspective that might be attributed to the flaring pixel dust explosions of Spacewar! 3.1 as well.
The most important of these changes, besides the addition of fuel consumption and the new, integrated hyperspace (see the next episode), was the adjustment of the velocity and the reload time of the torpedoes, effecting in an over-all faster paced gaming experience.
Here are the respective constants of Spacewar! 3.1 (shifts are scaling factors, lower shifts effect in greater velocity, counts give delays in frames):
Spacewar! 3.1: tno, 6, law i 41 / number of torps + 1 tvl, 7, sar 4s / torpedo velocity rlt, 10, law i 20 / torpedo reload time tlf, 11, law i 140 / torpedo life
and as extracted from Spacewar! 2b (the values are rather inlined in the code than placed in a constants table like in Spacewar! 3.1):
Spacewar! 2b: tno, law i 40 / number of torps + 1 tvl, sar 5s / torpedo velocity rlt, law i 40 / torpedo reload time tlf, law i 300 / torpedo life
As we may observed, the torpedo speed is doubled in version 3.1 (accordingly, the life time is now the half of what it was before, thus preserving the effective range) and the reload time is also shortened by a magnitude. Also new in Spacewar! 3.1 is the amount of torpedo space warpage, we explored above. By this, the most notable adoptions that were made in Spacewar! 3.1 attribute to the torpedoes, their behavior, and the consequent explosion of any collidible articles on the screen.
Vienna, September 2014
www.masswerk.at
In case you would have found any errors or inconsistencies, or would have additional information,
please contact me.
*****
◀ Previous: Part 6: Fatal Attraction — Gravity
▶ Next: Part 8: Hyperspace!
▲ Back to the index.