Inside Spacewar!
Part 3: Objects!
(Introduction · Colliding Objects · Starting a Flight · The Main Loop · Ending at the Beginning – Restart Checks · Scoring · Variations)
With a short delay (see the last entry) we resume our little software archeological approach to Spacewar!, the earliest known digital video game, and eventually arrive at the core logic of the game. Moreover, we'll finally meet some code by Steve Russell, the leading author of the project. Some may already know that this is the same Steve Russell who made Lisp a real programming language some years before, so we should be prepared for some indirectness and deferred logic — and some ingenuity as well. But there's even more to it: It is well known from interviews with various members of the Hingham Institute Study Group on Space Warfare that Spacewar! would have some kind of object oriented approach in its code. Notably, there was a table of "colliding objects" (Oral History of Steve Russell, interviewed by Al Kossow, rec. 9 Aug 2008, CHM catalog no. 102746453, p.13) holding the data and pointers to handling routines of the various moving objects (spaceships and torpedoes) to be handled by the main loop of the game. — Now, commonly a SIMULA program from 1965 is regarded as the very first object oriented program in history. Would this be another first by Spacewar!? And what would an objected oriented approach look like in assembler code? Let's see …
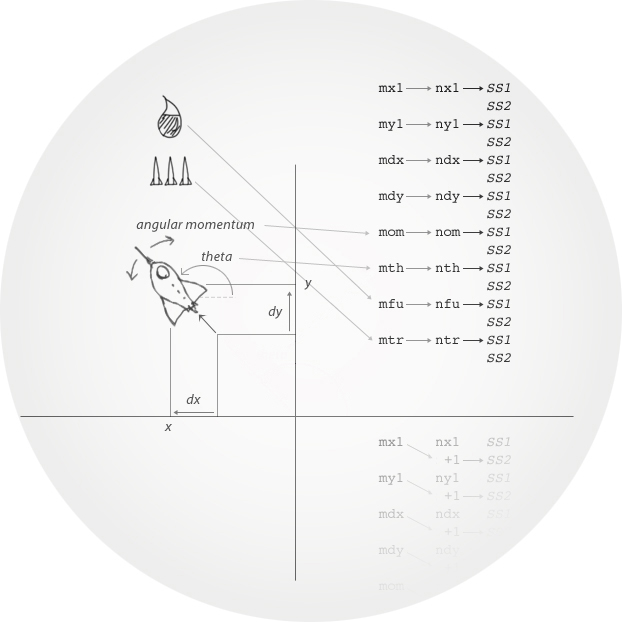
Objects in Spacewar!
BTW: ▶ You can play here the original code of Spacewar! running in an emulation.
Disclaimer/Credits: Spacewar! was conceived in 1961 by Martin Graetz, Stephen Russell, and Wayne Wiitanen. It was first realized on the PDP-1 in 1962 by Stephen Russell, Peter Samson, Dan Edwards, and Martin Graetz, together with Alan Kotok, Steve Piner, and Robert A Saunders. Spacewar! is in the public domain, but this credit paragraph must accompany all distributed versions of the program.
But before diving in the midst of the code, there's always a little other to be explored. This time, we're dealing with the second part of the Spacewar! source code, containing the main loop and logic of the game, and before having a look at the very beginning of this listing, we'll just jump to the very end of it.
This is, what it looks like (as usual, this is Spacewar! 3.1, considered the "standard version" here):
/ outlines of spaceships ot1, 111131 111111 111111 111163 311111 146111 111114 700000 . 5/ ot2, 013113 113111 116313 131111 161151 111633 365114 700000 . 5/ constants variables p, . 200/ / space for patches mtb, / table of objects and their properties start
(For the basics of PDP-1 instructions and Macro assembler code, please refer to Part 1.)
There some interesting things here: First, there is the data for the spaceship outlines, to be transformed by the outline compiler to a code producing a scaleable outline of the needle (ot1) and the wedge (ot2). We won't bother with the details here, leaving this for another episode.
Previously, we noted that constants and variables would be located by the assembler at the end of the code. Actually, this was a bit of a simplification: The space for both of them would be allocated anywhere, where the pseudo instructions constants and variables respectively would be encountered in the source, usually placed at the end of the code. This is followed by the pseudo instruction at label "p", advancing the program counter (or current location) by octal 200 addresses, leaving a gap reserved for future patches.
Right before the final "start" (which is rather marking the end of the sources), there's the line of our prime interest, a mere label "mtb". Lacking any instruction of its own, the label is just marking the very address at the end of the code, after constants, variables and an extra space for future additions. Even more interesting might be the comment associated to this label: This is using the terminology that would be introduced only years later, "objects" and "properties" — it's already there in 1962!
Colliding Objects
Thus prepared, we may have a look at the beginning of this second part of the source, right at label "ml0", a part of the code that is visited at the beginning of each iteration of the main loop (or frame) of the game. This is serving us with the very definition of this table und the structure of its objects:
spacewar 3.1 24 sep 62 pt. 2 /main control routine for spaceships nob=30 /total number of colliding objects ml0, load \mtc, -4000 /delay for loop init ml1, mtb /loc of calc routines add (nob dap mx1 / x nx1=mtb nob add (nob dap my1 / y ny1=nx1 nob add (nob dap ma1 / count for length of explosion or torp na1=ny1 nob add (nob dap mb1 / count of instructions taken by calc routine nb1=na1 nob add (nob dac \mdx / dx ndx=nb1 nob add (nob dac \mdy / dy ndy=ndx nob add (nob dap mom /angular velocity nom=ndy nob add (2 dap mth / angle nth=nom 2 add (2 dac \mfu /fuel nfu=nth 2 add (2 dac \mtr / no torps remaining ntr=nfu 2 add (2 dap mot / outline of spaceship not=ntr 2 add (2 dap mco / old control word nco=not 2 add (2 dac \mh1 nh1=nco 2 add (2 dac \mh2 nh2=nh1 2 add (2 dac \mh3 nh3=nh2 2 add (2 dac \mh4 nh4=nh3 2 nnn=nh4 2
There are two macros inserted right at the bginning, "load A, B" and "initialize, A, B" (here abbreviated to the first four significant characters "init"). Let's have a look at these first, just to know, what they would be doing:
define load A,B lio (B dio A term define initialize A,B law B dap A term
"load" is just setting the contents of the memory register with address A to the constant expression given by B. Likewise, "initialize" is setting the address part of the memory register A to the expression given in B. ("load" is using the IO register for this, while "initialize" is using the accumulator, but this is of not much significance here. But we may note that load is setting the whole contents of the memory register to a constant literal, while initialize is just setting the address part, preserving the intruction part as-is.)
So, what is this code all about? Actually, it's two strains of code at once. On the one hand, it's actually producing some machine code, on the other hand it's also defining en passant some values/labels internal to the Macro assembler for later use.
The very first expression, the pseudo instruction "nob=30" is declaring the number of objects, the table will hold. There will be a total of up to octal 30 (decimal 24) objects stored in this table.
nob=30 /total number of colliding objects ml0, load \mtc, -4000 /delay for loop init ml1, mtb /loc of calc routines add (nob dap mx1 / x nx1=mtb nob
The first instruction at ml0 is initilizing a count to the (octal) value -4000, a rough estimate of the instruction count used by the routines handling the spaceships. (This was an essential mechanism used to control the timing of the game in the absence of an internal clock: Each routine would add its instruction count to "\mtc" and any remaining number of instruction would be spent in a little loop at the end of each frame.)
The next few instructions are already presenting the general scheme of this structure:
"init ml1, mtb" initializes the address part of memory register ml1 to the address of mtb, the very end of the Spacewar! code and also the very first address of the table. We may note that this address is also left in the accumulator. "add (nob" adds the number of available objects to this and "dap mx1" deposits this sum into the address part of the instruction at mx1. Additionally, the pseudo instruction "nx1=mtb nob" defines "nx1" to point to the address at "mtb + nob". This scheme is then repeated over and over for various ms and ns sharing the same two trailing characters. At some point, the address is advanced only by a mere 2 memory registers, and at the last line nnn is defined to point to an address just after the very last address of the table.
add (nob dap my1 / y ny1=nx1 nob ... add (2 dap mth / angle nth=nom 2 ... add (2 dac \mh4 nh4=nh3 2 nnn=nh4 2
By this, we've set up a number of arrays of nob length (some of them only of 2 addresses length), one stacked upon the other. For each of them there's a label n.. defined, to point at the very first address of the array, and this address is also put in the address part at the corresponding label m.. at each traversal of this piece of code. Without too much of a spoiler, we may disclose that the m.. is associated with the current object handled by the loop. Thanks to the handy i-bit of the PDP-1, an instruction, say, "lac i mx1" would look up the address part of location mx1 and use this value as the actual address. In case the address part of mx1 would contain the address at nx1, we would load the contents of nx1 into the accumulator.
We may easily infer from the comments that each of these arrays will hold a specific property, with each of the objects using a value at a certain offset-index. We will refer to these entries as "slots", thus defining an object of the structure as composed of all the property entries sharing the same slot-index. By incrementing the address part of the m.. pointers (a single instruction on the PDP-1), we may easily refer to the next object, until we've reached the very last object at slot-index "nob-1".
Obviously, some of these properties are required for spaceships only. There is no such thing like a torpedo count or a turning angel for a torpedo. Thus we may save this space, giving the explanation for the last few entries advancing the base address just by 2. (Actually, Spacewar! 2b used a more orthogonal setup and reserved nob slots for each property anyway.) Moreover, we may conclude from this that the first two slots would be occupied by the spaceships, leaving (decimal) 22 slots for any torpedos.
The first slot (starting at mtb) would be special, encoding both the state and the handling routine (or, as we would call it today, the method) of the object. If zero, the object would be inactive. If non-zero, the address part would provide the address of the handling routine, linked dynamicly in the fashion of a state machine. The sign-bit would indicate, if the object might collide with other objects (unset), or if it would be in a special state, like in hyperspace or just exploding, where it would not interact with other objects (set).
On the functional side, traversed at the beginning of each frame, the code is initializing the various pointers to the addresses of the slots associated to the first spaceship.
Here's an overview of the resulting object allocation:
pointer address object semantics
(current obj.)
-----------------------------------------------------------------------------
ml1 mtb spaceship 1 state / object method (0: inactive)
mtb + 1 spaceship 2 (sign-bit: 0 .... collides,
mtb + 2 first torpedo 1 .... non-colliding)
... ...
mtb + 23 last torpedo
mx1 nx1 spaceship 1 position x-coordinate
nx1 + 1 spaceship 2
...
my1 ny1 spaceship 1 position y-coordinate
ny1 + 1 spaceship 2
...
ma1 na1 spaceship 1 duration (of explosion or torpedo)
na1 + 1 spaceship 2
...
mb1 nb1 spaceship 1 instruction count (of applied method)
nb1 + 1 spaceship 2
...
mdx ndx spaceship 1 delta x (of movement vector)
ndx + 1 spaceship 2
...
mdy ndy spaceship 1 delta y (of movement vector)
ndy + 1 spaceship 2
...
mom nom spaceship 1 angular velocity (turn rate)
nom + 1 spaceship 2
...
mth nth spaceship 1 theta (rotation angle, spacships only)
nth + 1 spaceship 2
\mfu nfu spaceship 1 fuel supply (negative, counting up)
nfu + 1 spaceship 2
\mtr ntr spaceship 1 torpedoes remaining
ntr + 1 spaceship 2
mot not spaceship 1 address of (compiled) outline code
not + 1 spaceship 2
mco nco spaceship 1 last control input
nco + 1 spaceship 2
\mh1 nh1 spaceship 1 hyperspace property 1
nh1 + 1 spaceship 2
\mh2 nh2 spaceship 1 hyperspace property 2
nh2 + 1 spaceship 2
\mh3 nh3 spaceship 1 hyperspace property 3
nh3 + 1 spaceship 2
\mh4 nh4 spaceship 1 hyperspace property 4
nh4 + 1 spaceship 2
nnn first address after table
Some of these "pointers" are just the address parts of instructions spreaded all over the code, while others (typically counters) are implemented as assembler variables (indicated by a leading backslash, designating a character decorated by an upper stroke in the original listing).
Now, does this qualify Spacewar! to comply to the term "object oriented"? Admittedly not in the exact sense Alan Kay would coin the term later. There are obviously some creteria missing, like an expressive object notation or any decent encapsulation, but these would be quite difficult to achieve in assembler code. On the other hand, prohibited these restrictions, we're not that far away from a C++ like notion of the term (heavily contested by Alan Kay as complying to the term at all). And we may even contemplate the origins of C on a DEC PDP machine in light of this example. So, if not object oriented to the letter, is it the first one avant la lettre? Not really. Mind Lisp (John McCarthy/Steve Russell 1958) and Sketchpad (Ivan Sutherland 1960-61). Is it amazing? Without question.
But, how could we appreciate the viurtues of this construct without seeing it in action? And how could we do better than just starting right at the beginning?
Spacewar! — Starting a Flight
When starting a session of Spacewar!, this is the code that we will hit at the very start of the program:
spacewar 3.1 24 sep 62 pt. 1 3/ jmp sbf / ignore seq. break jmp a40 jmp a1 / use test word for control, not iot 11 co[ntrol] / interesting and often changed constants /symb loc usual value (all instructions are executed, / and may be replaced by jda or jsp) tno, 6, law i 41 / number of torps + 1 tvl, 7, sar 4s / torpedo velocity rlt, 10, law i 20 / torpedo reload time tlf, 11, law i 140 / torpedo life foo, 12, -20000 / fuel supply maa, 13, 10 / spaceship angular acceleration sac, 14, sar 4s / spaceship acceleration str, 15, 1 / star capture radius me1, 16, 6000 / collision "radius" me2, 17, 3000 / above/2 ddd, 20, -0 / 0 to save space for ddt the, 21, sar 9s / amount of torpedo space warpage mhs, 22, law i 10 / number of hyperspace shots hd1, 23, law i 40 / time in hyperspace before breakout hd2, 24, law i 100 / time in hyperspace breakout hd3, 25, law i 200 / time to recharge hyperfield generators hr1, 26, scl 9s / scale on hyperspatial displacement hr2, 27, scl 4s / scale on hyperspatially induced velocity hur, 30, 40000 / hyperspatial uncertancy ran, 31, 0 / random number / place to build a private control word routine. / it should leave the control word in the io as follows. / high order 4 bits, rotate ccw, rotate cw, (both mean hyperspace) / fire rocket, and fire torpedo. Low order 4 bits, same for / other ship. Routine is entered by jsp cwg. 40/ cwr, jmp mg1 / normally iot 11 control . 20/ / space / routine to flush sequence breaks, if they occur. sbf, tyi lio 2 lac 0 lsm jmp i 1
The first four instructions at the very four lowest addresses of the PDP-1's memory were reserved for the sequence break system (or, as we would call it today, interrupts): In case a perpheral device would send a sequence break signal, the CPU would dump the contents of the accumulator into address 0, the value of the program counter into address 1, and the contents of the IO register into address 2. Then it would execute the instruction at address 3 in order to react to the break. The very first line of code "3/ jmp sbf" is just setting a handler for this case, a jump to the label sbf. And peeking ahead to the very end of this snippet, the code at sbf is just doing what is indicated by the comment, resuming from the break by essentially ignoring it. (tyi resets the input state of the Flexwriter and the following lines are restoring the contents of the two CPU registers and jump to where the program had been interrupted by the break.)
Due to this sequence break mechanism the default start address of any PDP-1 program was assumed to be at address 4. This is a jump to the label a40 as in "jmp a40". This is followed by an alternate entry point at address 5, which, as indicated by the comment, would configure the program for use of the console's test-word switches as the source for input, rather than reading the state of MIT's custom control boxes.
This is followed by another table, this time defining some "interesting constants" or parameters, controlling the game's behavior. Each line is starting with a label, followed by the address, an instruction or value, and an informative comment. We may note that some of these entries are actually instructions (like a bit-wise shift right, scaling a factor by the given amount), to be executed in the course of the program.
The use of these paramters is illustrated by a quote from Hackers. Heroes of the Computer Revolution (Levy, Steven, 1984/2010, pp.53):
The variations were endless. By switching a few parameters you could turn the game into "hydraulic Spacewar," in which torpedoes flow out in ejaculatory streams instead of one by one. Or, as the night grew later and people became locked into interstellar mode, someone might shout, "Let's turn on the Winds of Space!" and someone would hack up a warping factor which would force players to make adjustments every time they moved.
Located right at the beginning, it would have been be quite easy onto put the contents of these locations to the control console, by adjusting the (bit-wise) switches of the test-address, then adjusting the contents of this location by the test-word switches, and injecting this right back into the PDP-1's core memory on the fly. "Hydraulic Spacewar" would be achieved by setting label rlt (octal address 10) to a rather low value, "Winds of Space" would be likewise set up, by adjusting the value-part of the instruction at the (octal address 21) to a rather low value (with the default value being the maximum scaling factor, effecting in straight trajectories).
Framed by a few spare locations for later patches we find the actual input routine for reading the control boxes at label cwr, a jump vector to label mg1. (We may already note an extreme indirectness of the input method, which is also emphasized by the comments explaining the encoding of the control word and the various spaces reserved for patching this. Obviously, expectations were high for other methods of input to come, for the benefit of future space pilots.)
By this, we're done with the first part of the lising and pick up the code at label a40, to which we were redirected by executing the instruction at the default start address 4.
a1, law mg2 / test word control dac \cwg jmp a a40, law cwr / here from start at 4 dac \cwg jmp a6 a, // code handling the end of a game, skipped here ... a6, // code handling the start of a game, skipped here ...
The code at a40 is an easy one: it copies the address of the location labeled cwr (we've already seen above) to the varaible \cwg by loading it into the accumulator and depositing it in the target address. This is followed by jump to label a6.
Above, we can also see the the setup for the test-word controls: Here, the address labeled mg1 is copied to \cwg. Thus the control-word getter \cwg is aliasing the effective input routine. This time, the setup is followed by a jump to label a.
The code at label a is handling the end of a game and any of the rudementary score display. The code entered at a6 is parsing and storing the current state of the control-word for this purpose. As this is not essential to the game — this was actually just a patch to Spacewar! 2b, apparently now lost — we're skipping this here in order to fast forward to the actual setup sequence at label a2, following immediately to this.
a2, clear mtb, nnn-1 / clear out all tables law ss1 dac mtb law ss2 dac mtb 1 lac (200000 dac nx1 dac ny1 cma dac nx1 1 dac ny1 1 lac (144420 dac nth
The pseudo instruction clear inserts a macro in place, which is resetting the contents all locations from mtb up to nnn-1 to zero (0):
define clear A,B init .+2, A dzm index .-1, (dzm B+1, .-1 term
Wait a moment, this is inserting two other macros, initialize and index!
This is, what it would look like, when expanded:
cl0, law mtb dap cl0+2 dzm cl1, idx cl1-1 sas (dzm nnn-1+1 jmp cl1-1
We starting with loading the address mtb, the very first location of the objects table, into the accumulator and depositing this in the address part of the dzm instruction. Then, we're executing the dzm (deposit zero in contents) on this address. The next instruction increments the address part of the instruction immediately previous to this by one, also leaving the incremented contents of this location in the accumulator. The instruction "sas (dzm nnn-1+1" is a conditional skip, comparing the contents of the accumulator to an dzm instruction on location nnn. If not equal, the next instruction jumps back to the dzm instruction to be executed on the incremented address again. If equal, we're done and will continue with the instruction following the macro.
This may seam a bit overly complicated, but it really shows, how the macros would be treated as atomic building blocks, quite like statements of a higher level language. Anyway, let's have a look at the rest of this snippet:
(Comments starting with double slashes are mine, N.L.)
a2, clear mtb, nnn-1 / clear out all tables law ss1 // code handling spaceship 1 dac mtb // store in mtb law ss2 // code handling spaceship 2 dac mtb 1 // store in mtb+1 lac (200000 // half distance between origin and max dac nx1 // spaceship 1 - x dac ny1 // spaceship 1 - y cma // complement to -200000 dac nx1 1 // spaceship 2 - x dac ny1 1 // spaceship 2 - y lac (144420 // 180 deg dac nth // spaceship 1 - theta
Having reset all table entries (object properties) to zero, we're going to initialize some of them to useful values. First, the object routines of the two spaceships (at mtb and mtb+1) are set up to point to the normal spacship handling routines at ss1 for spaceship 1 and ss2 for spaceship 2 respectively. Then, the constant value of (octal) 200000 is loaded into the accumulator. This is half the extent of the internal coordinate system of the game in any direction along the two axis. This is stored in the x and y slots setting up the start position of the first spaceship. Then, this value is complemented by the instruction cma (complement AC), giving a position in the opposite direction of the central origin (-200000), and stored as the positon of spaceship 2 (as in nx1+1 and ny1+1). Finally, the constant value 144420 (representing an angle of 180°) is stored as the current angle (theta) of spaceship 1 in location nth, leaving the angle of spaceship 2 at zero.
(This is already conveying some idea, how the data is represented internally: The value 144420 isn't any other than the octal notation of b001100100100010000, an estimate of Pi with the fractional point after bit 3 and at a precision of 12 bits. The position of half the distance along an axes to one side is 400 shifted 8 bits to the left. As we know from the previous episodes, this is the format used to provide positions to the dpy instruction. Thus, angles are measured in radiants and positions are mapped to screen coordinates in the range -377777..+377777 along the two axes. Thanks to the 18 bit one's complement number representation of the PDP-1, toroidal space — popping up at the other side when crossing the borders of the screen — will come for free: By adding 1 to 377777, we'll end up at 400000, or -377777; likewise the other way round. Of these 18 bits only the highest 10 ones will be used by the display, with the lower 8 bits just ignored.)
Before we continue, we might recall having seen the two tables encoding the outlines of the spaceships near the end of the program listing. This encoding was quite handy when it came to experimenting with different shapes for the two ships, but with the addition of the runtime-expensive code for gravity, the program was driven above flicker-free display performance. In order to preserve the changable outlines and still maintaining some decent performance, an ingenious outliner compiler was introduced by Dan Edwards, replacing Steve Russell's original interpreter routine. (And, in deed, spaceship hacking would become a favorite hobby of virtual space pilots, thanks to Dan Edwards' virtuousity.)
The following instructions are calling the outline compiler to produce and store the code drawing the spaceships:
law nnn / start of outline program dac not lio ddd spi i jmp a3 jda oc / compile outline ot1 a3, dac not 1 jda oc ot2
We're dealing here with the problem of having to pass at least two values to the compiler, the address, where the code should go, and the location of the data table describing the outline of a ship. Moreover, we should know, where the generated code actually ends and the next one would begin (since different shapes would produce code of different length, depending on the complexity of the outline), so we're expecting a return value from the compiler. How could this be achieved?
"law nnn" loads the address of the location just after the end of the colliding objects table into the accumulator, which is then deposited in the slot containing the address of the outline code for the first spaceship at not. Leaving the next three instruction out of consideration for the moment, the instruction "jda oc" is calling the outline compiler at oc. The instruction jda is quite a nifty one: It deposits the contents of the accumulator into the given address and performs a jump-to-subroutine to the location immediately following to this address. By doing so, it puts the current value of the program counter + 1 into the accumulator to be used as the return address. But at this location a bare "ot1" is inserting the address of the outline table for spaceship 1 in place. By this, we just accomplished our passing of arguments: the address of the code to be placed at is now in oc and the location of the data is in the accumulator. The outline compiler returns at the instruction next to this (the return address + 1) and we may infer from the code at label a3 — which is performing the same procedure for the second spaceship — that the address of the location following immediately next to the compiled code would be passed in the accumulator, since this is the value deposited as the start address of the outline code of spaceship 2. (This might be the right time for an exclamation of choice, I'll go with a Whoopee.)
So, what are the three instructions doing, we just skipped?
lio ddd // reserve space for another ship? load ddd into IO spi i // sign bit set? (skip on contents of IO not positive) jmp a3 // no, use same outline
This is loading the value at label ddd into the IO register and skips a jump to label a3, if this value would be negative. If the sign-bit would not be set, we'll take the jump to a3, reusing the same data (as stored in the accumulator) for the second spaceship, resulting in a game with both ships to be displayed as wedges. — In case you would wonder, label ddd is to be found right in the constants table and is set to -0, setting up a game using individual outlines for the ships.
(But, why would you want to have a single outline for both of the ships? There's a good reason to do so, as we learn from the comment on constant "ddd", "0 to save space for ddt". "ddt" happens to be MIT's online debugging program. So, this was the development setup and a true hacker in hacking mode would have seen Spacewar! with two wedges on the screen.)
By this, we're nearly done with the setup, leaving just a few properties to be initialized:
xct tno // load minus the number of torps + 1 (41) dac ntr dac ntr 1 lac foo // load fuel supply (-20000) dac nfu dac nfu+1 law 2000 // default instruction count per ship dac nb1 dac nb1 1 xct mhs // load number of hyperspace shots (10) dac nh2 dac nh2 1 jmp ml0 // enter the main loop
The instruction xct (execute instruction in address) is yet another indirect instruction, executing the instruction given in the address part, in this case "tno" ("number of torps + 1") as defined in the constants table. This is a simple "law i 41", loading the value -41 (decimal -33) into the accumulator. The next two instructions are storing this as the properties for the torpedo count of the two ships at ntr and ntr+1 respectively. Quite similarly, the amount of fuel is setup in nfu and nfu+1 from the value in foo. Finally, the instruction count (at nb1 and nb1+1) is set to the constant 2000 and the number of possible hyperspace shots (at nh2 and nh2+1) is setup by executing the instruction at mhs, also to be found in the constants table. Having the two ships initialized and setup nicely, we're jumping to label ml0, setting up the various object pointers to the properties of the first spaceship, as we've already seen above.
— Lift off! —
The Main Loop
Each frame starts at label ml0, with its algorithmic strain initializing the various "pointers" to the properties of the first spacship.
(Thus, we're starting with the following relations, each address part of the locations referring to the current object pointing to the very first slot at the base address of each of the related properties: ml1 ⇒ mtb, mx1 ⇒ nx1, my1 ⇒ ny1, ma1 ⇒ na1, mb1 ⇒ nb1, mdx ⇒ ndx, mom ⇒ nom, mth ⇒ nth, \mfu ⇒ nfu, \mtr ⇒ ntr, mot ⇒ not, mco ⇒ nco, \mh1 ⇒ nh1, etc.)
The code directly following to this is handling any end-of-game or restart conditions as well as scoring. These were essentially patches to Spacewar! 2b, now incorporated in the core logic of version 3.1. Since they are not essential to the logic of the game, we'll skip them here to cover them a bit later in favor of the greater picture. We're picking up the flow of events at label ml1. This is, what the rest of this loop looks like:
ml1, lac . / 1st control word sza i / zero if not active jmp mq1 / not active swap idx \moc spi jmp mq4 law 1 add ml1 dap ml2 law 1 add mx1 dap mx2 law 1 add my1 dap my2 law 1 add ma1 dap ma2 law 1 add mb1 dap mb2 mot, lac . dap sp5 ml2, lac . / 2nd control word spq / can it collide? jmp mq2 / no mx1, lac . / calc if collision mx2, sub . / delta x spa / take abs val cma dac \mt1 sub me1 / < EPSILON ? sma jmp mq2 / no my1, lac . my2, sub . spa cma sub me1 / < epsilon ? sma jmp mq2 / no add \mt1 sub me2 sma jmp mq2 lac (mex 400000 / yes, EXPLODE dac i ml1 / replace calc routine with explosion dac i ml2 lac i mb1 / duration of explosion mb2, add . cma sar 8s add (1 ma1, dac . ma2, dac . mq2, idx mx2 / end of comparison loop idx my2 idx ma2 idx mb2 index ml2, (lac mtb nob, ml2 mq4, lac i ml1 / routine for calculating spaceship dap . 1 / or other object and displaying it jsp . mb1, lac . / alter count of number of instructions add \mtc dac \mtc mq1, idx mx1 / end of comparison and display loop idx my1 idx ma1 idx mb1 idx \mdx idx \mdy idx mom idx mth idx \mas idx \mfu idx \mtr idx mot idx mco idx \mh1 idx \mh2 idx \mh3 idx \mh4 index ml1, (lac mtb nob-1, ml1 lac i ml1 / display and compute last point sza i / if active jmp mq3 dap . 1 jsp . lac i mb1 add \mtc dac \mtc mq3, background / display stars of the heavens jsp blp / display massive star count \mtc, . / use up rest of time of main loop jmp ml0 / repeat whole works
As we'll soon discover, these are actually two nested loops: An outer loop iterating over all the objects and an inner loop, comparing an object's position to those of any objects with an higher index in order to detect any collisions. At ml1, we're dealing with the setup of the inner loop: The address part of location ml1 is already pointing to the "handling" property (encoding the status and/or handling method) of the current object (the original comments are using the term "control word" for both the input reading and the handling property of an object, which might be a bit confusing).
ml1, lac . / 1st control word sza i / zero if not active jmp mq1 / not active (// iterate outer loop, next object) swap // macro, exchanges contents of AC and IO idx \moc // \moc is else unused! spi // is it collidable? (skips, if control word plus) jmp mq4 // no - no comparison, but handle object law 1 add ml1 dap ml2 // ml2 = ml1 + 1 law 1 add mx1 dap mx2 // mx2 = mx1 + 1 law 1 add my1 dap my2 // my2 = my1 + 1 law 1 add ma1 dap ma2 // ma2 = ma1 + 1 law 1 add mb1 dap mb2 // mb2 = mb1 + 1
The first instruction loads the current object-handle ("control word") into the accumulator. The next two instructions test, if this would be active (not zero) or (zero). "spa i" is a conditional skip, if the contents of the accumulator would not be zero (mind the negating i-bit). If zero, we'll take the jump to mq1 at the next instruction to start over with the next object.
If still in business, things are getting a bit enigmatic: "swap" is a macro, exchanging the contents of the accumulator and the IO register. (We've seen this already in Part 2, accomplished by two instructions "rcl 9s".) The next instruction is incrementing the contents of variable \moc, a token that isn't used anywhere else in the source.
— When this is without any effect, why would this be here? There are some plausible reasons for this:
- Leftovers from a previous version. (But this wasn't there in Spacewar! 2b, leaving the lost version 3.0 as the single canditate.) We might take in consideration that this was developed quite busily and before there were any nice on-screen editors.
- A provision for patches (earlier patches, or patches expected to come). E.g. Spacewar! 2b was setting up and iterating some variables and properties for hyperspace (
\mh1..\mh3andnh1..nh3), while there wasn't any hyperspace at all. We could imagine a conversation like this: "Hey Martin, what would would you need for hyperspace?" — "Hum, three variables per object at least, Slug."
Applicable to both of these explanations, there's an account on a version featuring a "slight change in background star luminosity for hyperspace jumps". Maybe this would have been controlled by the counter \moc.
Anyway, the "control word" is now in the IO register, thanks to the previous swap. The next instruction "spi" (skip on plus IO) skips, if the sign bit would not be set. If set, this would be the signal for the object not being in collidable state, so we won't compare positions and jump to the actual object handling at label mq4.
Now, we're setting up some locations for the comparison, by depositing the addresses of the next object (the one with the next slot-index) in ml2 ("control word"), mx2 (x-position), my2 (y-position), ma2 (duration), and mb2 (instruction count). If we started with the first spaceship as the current object, the various locations would point to the properties of the second one.
mot, lac . // address of compiled outline code
dap sp5
This is setting up the address of the outline code for the current object's shape in the address part of location sp5. (We could muse on the reasons for this instruction being placed here, since we're also itereating over any torpedoes here, without any outline code at all. Furthermore, sp5 isn't addressed by any other piece of code, but the jump instruction in place at this label. Thus, sp5 could have been mot from the beginning. Anyway, this is doing no harm and we may presume similar reasons for this piece of code as we mentioned for the variable \mco above.)
Now, it's time for the actual collision detection, first in x-dimension:
ml2, lac . / 2nd control word spq / can it collide? jmp mq2 / no mx1, lac . / calc if collision mx2, sub . / delta x spa / take abs val cma dac \mt1 sub me1 / < EPSILON ? sma jmp mq2 / no
The first three instructions repeat the pattern we've seen above: load the "control word", check if it is positive (collidable), if not, jump to mq2.
At mx1 the x-position of the current object is loaded into the accumulator (the address having been inserted previously in place) and the sub at mx2 subtracts the x-position from the second object from this. Now we make this an absolute value: spa skips, if the value would be already positive. If not, cma complements the contents of the accumulator, resulting in the 1's complement, converting the negative number format used by the PDP-1 into a positive one.
The absolute delta x is now stored in variable \mt1 and compared to the constant me1 (we've seen this in the constants table earlier) by subtracting this collision range. Instruction sma skips on minus AC, thus indicating that the delta x would be smaller than our epsilon. If not, there is no collision and we jump to mq2.
This is then repeated for delta y:
my1, lac . // y my2, sub . // delta y spa // take abs val cma sub me1 / < epsilon ? sma jmp mq2 / no
If we haven't made the jump to mq2 yet, the compared object is inside a square of 2 x me1 width around our current object. But this isn't really satisfying, since this would not be handling any rotations of our elongated ships. If we just could do something more like a circular hit box, but without all this expensive math ...
add \mt1 // dx + dy sub me2 // < epsilon #2 (epsilon/2) ? sma jmp mq2 // no
(Note: The next three paragraphs have been re-edited in Oct. 2016.)
What's happening here? By adding Hitboxes in Spacewar!\mth1, the absolute value of delta x, to the difference of the absolute value of delta y and me1 we arrive at a value that will be substantially only, if both delta x and delta y are of substance. In other words, we're checking, if (me1 + me2) < abs(dx) + abs(dy).
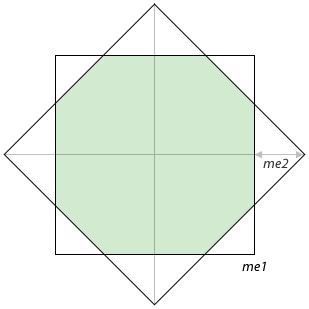
( me1 ≥ |dx| ) & ( me1 ≥ |dy| ) & ( me2 ≥ |dy| - me1 + |dx| )
With me2 defined as exactly half the value of me1, we're effectively clipping the corners of our previously square hitbox for an octogonal hit area. (And that's also, what it's meant to be, compare Oral History of Steve Russell, interviewed by Al Kossow, rec. 9 Aug 2008, CHM catalog no. 102746453, p.13.)
And this is working exceptionally well, as can be admired while playing the game. — However, Spacewar!'s authors never claimed to do any hit-detection at all, as the torpedoes were said to be equipped with "a proximity fuze which causes the torpedo to explode when it comes within a certain critical distance of any other collidable object which will also be caused to explode." (J. M. Graetz, "Spacewar! Real-Time Capability of the PDP-1", DECUS Proceedings 1962, p.37) (But we are not obliged to take this as just a humble understatement, since this is also how earthly anti-aircraft missiles do it. Thus, this claim may be due to some sense of realism of the simulation, too.) — Anyway, if we just made the last skip, we're inside the second hitbox as well, and detected a collision.
Time for an explosion:
lac (mex 400000 / yes, EXPLODE dac i ml1 / replace calc routine with explosion dac i ml2 lac i mb1 / duration of explosion (// instruction count = 2000) mb2, add . // 2 spaceships: 4000 in AC, spaceship/torp: 2020 cma // make it negative for count up sar 8s // -4000 >> 10 = -10, spaceship/torp: -4 add (1 // -7 / -3 ma1, dac . // duration of explosion, first object ma2, dac . // duration of explosion, second object
The first instruction sets up the handling-property ("control word") for the explosion by loading the address of the explosion routine (mex) and setting the sign-bit (400000) in the accumulator. (Since the sign-bit is set, an exploding object is not collidible and you may pilot safely through the debris of your exploding opponent.) This is now stored in the status property of the two colliding objects. (Mind the i-bit, resulting in the addresses being used for another address lookup: This is not depositing the contents of AC in locations ml1 or ml2, but in the locations their address parts are pointing to, the "slots" in the object table.)
Having thus replaced the normal object-method by the explosion routine, we're now setting up the timing for the explosion. For this, we load the contents of the address in mb1, the instruction count of the first object, into the accumulator and add the instruction count of the second one to it. (This has been put in place previously during the setup of the comparison loop.) If the two objects would be the two spaceships, this would be 4000. With a torpedo's instruction count of 20, this would make 2020 for a spaceship hit by a torpedo and a mere 40 for a torpedo hitting another one. This is complemented, since the value in the address refered to by ma1 and ma2 will be used for a count up. Then, a "sar 8s" scales down to either (decimal) -8, -4, or just a minus zero (for two torpedoes) and by adding the constant 1, we get the final frame count. Thus, a spaceship hitting another one will result in a big explosion, twice the length of a spaceship hit by a torpedo, while the explosion resulting from a collision of two torpedoes will be over after the first frame. With both objects having assigned this value in their timing slot, the explosion is set up and ready to be displayed.
Having the collision handled, we meet again with all the excluded cases at label mq2, the iterating part of the comparison loop:
mq2, idx mx2 / end of comparison loop idx my2 idx ma2 idx mb2 index ml2, (lac mtb nob, ml2
The first 4 instruction are incrementing the values in mx2, my2, ma2, and mb2, with their address parts now pointing to the properties of the next object to be compared. The last pseudo instruction inserts a macro which increments ml2 (the next "control-word") and compares the result to the constant expression "lac mtb nob". (Remember the instruction part of mb2 being a lac?) If still in the range of our number of objects (nob), we'll jump to mb2 and check for another collision. If we've reached the last of our objects, we fall through, to finally call the handling routine currently linked to our object:
mq4, lac i ml1 / routine for calculating spaceship dap . 1 / or other object and displaying it jsp . mb1, lac . / alter count of number of instructions add \mtc dac \mtc
This loads once more the "control word" into the accumulator and then deposits just the address part in the location immediately after the dap instruction. (Thus, we have not to worry about the sign-bit.) Finally, the routine at this address (whatever this might be) is executed by the jsr.
The flow of control returns from this handling routine at label mb1, where the estimated instruction count is loaded into the accumulator. After adding the value in \mtc to this (being the negative total instruction count per frame, initially set to -4000 at ml0), we're storing the updated amount in \mtc.
Now it's time to iterate the outer loop, joining any branches that left earlier by a jump to mq1:
mq1, idx mx1 / end of comparison and display loop idx my1 idx ma1 idx mb1 idx \mdx idx \mdy idx mom idx mth idx \mas idx \mfu idx \mtr idx mot idx mco idx \mh1 idx \mh2 idx \mh3 idx \mh4 index ml1, (lac mtb nob-1, ml1
This is iterating all the pointers just like we've seen before, but this time for the current object. (Note that this is just incrementing the various pointer addresses. It doesn't matter that there's no space reserved in the objects table for the angle or the fuel supply of a torpedo as long as these properties are not accessed.) We may note the little difference in the end condition of the loop, cheking now a top-offset of "nob-1". Since there is no need to compare the very last object to any further one, it is not handled inside the loop, but left for the last few instructions, providing just the object handling (same as we've seen above):
lac i ml1 / display and compute last point sza i / if active jmp mq3 dap . 1 jsp . lac i mb1 add \mtc dac \mtc
(We may note Steve Russell's brute realism in the comment: Not a torpedo (this could not be any other kind of object), but just a "point".)
Having handled this last object, we arrive close to the end of the frame. Time to take care of all the other entities to be displayed on the scope. Namely the Expensive Planetarium (see Part 1) and the "heavy star" (see Part 2):
mq3, background / display stars of the heavens jsp blp / display massive star count \mtc, . / use up rest of time of main loop jmp ml0 / repeat whole works
With all the heavy work done, the macro count is spending any instructions left in a tiny loop, in order to stabilize the frame rate:
define count A,B isp A jmp B term
(This is, as we will see, a quite important macro to Spacewar!, giving the explanation, why all those counts are negative: isp increments the contents of the given address and skips, if the the result would be positive. If still negative, the jump to A, here a stop referring to the very location the macro is inserted at, happening to be the isp instruction. Otherwise, we fall through to the next instruction after the macro.)
The final "jmp ml0" starts the next frame with a jump to ml0, the setup of the outer loop.
Ending at the Beginning
So, we're finally through — but wait, haven't we skipped a few instructions right at the beginning?
Since there isn't any other context where this would fit, we're going to discuss this parts here, too.
The first one, following directly the initialization of the main loop at ml0, is checking for the end of a game:
(As usual, the comments with double slasshes are mine; N.L.)
law ss1 // load address of routine for spaceship 1 xor mtb // compare to current value in mtb sza // still the same? jmp mdn // no, game over law ss2 // load address of routine for spaceship 2 xor mtb 1 // compare to current value in mtb+1 sza // still the same? jmp mdn // no, game over law 1 / test if both ships out of torps add ntr // add 1 to remaining torpedoes of spaceship 1 spa // exhausted ? jmp md1 // no, game is still running law 1 // add 1 to torpedoes of spaceship 2 add ntr 1 spa i // exhausted ? jmp mdn // yes, game over
As may be concluded from the comments, this checks
a) for the object-routines of the two spaceships still pointing to the standard routine by performing an exclusive OR (if there's a difference, the ship is exploding or inactive), or
b) if the torpedo count of both ships would be -1 or higher.
(Remember the constants table reading "number of torps + 1"?)
Should any of these conditions be met, we would jump to mdn. If not, we either jump explicitly to md1 or skip to this location by the last "spa i":
md1, xct tlf / restart delay is 2X torpedo life sal 1s dac \ntd jmp ml1
So, at the beginning of every frame with both the ships in play, the variable \ntd will be set to twice the torpedo life by executing the instruction at tlf ("law i 140"), shifting the result 1 bit to the left, and finally storing this in \ntd. As we are learning from the comment, this is the restart delay, reset each frame of normal gameplay.
So, what's happening at the end of a game?
Scoring
mdn, count \ntd,ml1 // jump to ml1, counting up \ntd stf 1 // set flags 1 and 2 stf 2 law ss1 // load address ss1 xor mtb // compare to mtb sza clf 1 // if not equal, clear flag 1 sza i idx \1sc // if equal, increment score for spaceship 1 law ss2 // load address of ss2 xor mtb 1 // compare to mtb+1 sza clf 2 // if not equal, clear flag 2 sza i idx \2sc // if equal, inc score of spaceship 2 clf 2 // clear flag 2 anyway (?) jmp a
The macro count in the first instruction is counting up the restart delay, we've just set up previously. If still negative, we jump to normal operations in order to display the explosions and provide a little gap for the players to catch breath.
Otherwise, we're dealing with the scores, kept in \1sc and \2sc for spaceship 1 and spaceship 2 respectively. The mechanism is essentially the same as above, but now the score of any surviving ship is incremented. Also, both program flags 1 and 2 are set at the beginning, and cleared, if the associated ship would be inactive (dead). Interestingly, these flags are never checked and flag 2 is cleaned up at the end, regardless of the survival of spaceship 2. Opposed to this, flag 1 is left as-is, without any clean up done. What's happening here?
Now, these two parts were patches in Spacewar! 2b, the first one being an improved version of the auto-restart patch of 2b, this second one would have been the (apparently lost) scoring patch mentioned in "The Origin of Spacewar" by J. M. Graetz.
Typically we find the use of flags in encapsulated parts of Spacewar!, like the Expensive Planetarium or the code for the gravitational star, both of which we have seen before in the previos episodes. Opposed to this, there's not a single case in the main part of the program, where a program flag would be checked. This is another clue for this being either imported straight forward from a patch, which would have to check the state of the ships a bit later again, or this being set up to communicate with another patch, we don't know anything about.
Another plausible purpose of this setting and clearing of flags would be the display of the outcome of the last game by the lights for the program flags on the control console (see the illustration below). But this would have been hindered by the last unconditional clearing of flag 2.
Anyway, we'll jump from here to label a, just after the initial setup of the input methods (using the control boxes or the test-word switches):
a, lac \gct // load contents of \gct sma // sign-bit set? jmp a5 // no, jump to a5 count \gct, a5 // increment \gct, jump to a5, while minus lac \1sc // load score 1 sas \2sc // skip on score 2 eq score 1 jmp a4 // jump to score display law i 1 // it's a tie, reset \gct to -1 dac \gct a5, lat // load testword and check bit 12 and (40 sza i jmp a2 // not set, jump a2 (new game) a4, lac \1sc // score display in AC (spaceship 1) lio \2sc // and IO (spaceship 2) hlt // halt lat // check testword (bit 12) again and (40 sza jmp a2 // if set, jump to new game dzm \1sc // else clear scores dzm \2sc a6, lat // init \gct from testword rar 6s // shift right 6 bits and (37 // any of the lower 5 bits bits set? (testword 7..11) sza cma // yes, complement AC (now in range -37 .. -1) dac \gct // deposit in \gtc
This is all about the score display, the very heart of it being the instructions at labels a5 and a4: At a5 the instruction lat is loading the test-word and we check bit 12 (the 6th switch from the right) for being set. If so, we'll display the scores at a4, else we'll start over for a new game at a2 without delay.
The code at a4 is actually displaying the scores at the control lights of the console (in binary), using the accumulator to display the score of spaceship 1 and IO for spaceship 2, and pauses by a halt instruction. When resumed (by the continue switch on the console), bit 12 of the test-word is checked again. If (still) set, we'll jump to a new game, else the scores are cleared for a new match.
But what is all this business about \gct above and below?
This is quite a nifty one, and it's a provision to set up a match of a specified number of games, stored as a negative number in \gct (game count?):
First, we'll have to remember that the test-word is also a possible source of control input, for which the 4 outer most bits (0..3 and 14..17) are used. As we've already seen, bit 12 (the 6th switch from the right) is used to check for the scores to be displayed after a game. Moreover, the next 5 bits are used to set up a match of up to dezimal 31 (octal 37) games. For this, the middle 5 bits of the test-word are checked at a6. If any of them would be set, these are moved to the lower position by a shift by 6 bits to the right and stored as a negative number in \gct to start a new match.
At the end of a game, we arrived at label a located at the top of this snippet. Here \gct is checked for containing a negative number, indicating that this would be an ongoing match. If so, the game counter \gct is incremented and, when still negative, we'll jump to a5, checking bit 12 of the test-word as described above. In case the counter would have been incremented to zero, we'll check for the match being a tie. If so, we'll add another game by setting \gct to -1. Otherwise, we'll jump immediately to a4 to display the final score, without another check for test-word bit 12.
Thus, a match may be set up to be of a number of games specified by the 5 middle switches of the test-word. Would the switch for bit 12 be set, scores are displayed after each game, otherwise only at the end of a match (resolving any ties by a sudden death). If the switch for bit 12 would be not set (as in normal match play) the scores are cleared after a match and the whole counting starts over. If there's no match, the switch for bit 12 provides cumulative scores in a single game mode, until cleared by the switch being reversed before resuming the halted game.

The control console of the DEC PDP-1. Mind the test-word switches at the bottom.
(Image credits: Marcin Wichary, 2008, CreativeCommons, edited N.L. 2014)
Test Word Layout in Spacewar! bits: 0 1 2' 3 4 5' 6 7 8' 9 10 11'12 13 14'15 16 17 usage: -PLAYER 1- GAMES P. MATCH SC -PLAYER 2- semantics: L R T F 16 8 4 2 1 L R T F | | => 0..31 GAMES | | HYPERSPACE HYPERSPACE SC: Show scores in single game mode or after the last game in match mode. If cleared, when resumed from the halt for the score display, scores are reset.
(Update: There is actually some room for improvement in the starting sequence as related to scoring, as indicated by a handwritten rearrangement of label a6 — probably by Martin Graetz — annotated to a listing of Spacewar! 3.1 that has surfaced recently: While the entry point for the game with test-word controls is routing the code through all the scoring evaluations, the normal entry point for starting the game with control boxes jumps to label a6. Now, label a6 happens to be located just after the initial clearing of the scores for the two spaceships, wheras it would be preferable to have them cleared (mind the persistent core memory of the PDP-1), when restarting a game, too. For this we would want to move label a6 2 instructions up in the source code.)
Variations
As usual, we won't close without having a look at variations of the main theme, this time in Spacewar! 4.8, the last known version of the original Spacewar!:
spacewar 4.8 7/24/63 pt. 2 dfw nob=30 /total number of colliding objects ml0, setup \mtc, 5000 /delay for loop init ml1, mtb /loc of calc routines init mx1, nx1 /x init my1, ny1 /y init ma1, na1 /count for length of explosion or torp init mb1, nb1 /time taken by calc routine init mdx, ndx /dx init mdy, ndy /dy init mom, nom /angular velocity init mth, nth /angle init mfu, nfu /fuel init mtr, ntr /number torps remaining init mot, not /outline of spaceship init mco, nco /old control word law nh1 dac \mh1 law nh2 dac \mh2 law nh3 dac \mh3 law nh4 dac \mh4 // snip (the loop) variables constants mtb, / table of objects and their properties nx1=mtb nob ny1=nx1 nob na1=ny1 nob nb1=na1 nob ndx=nb1 nob ndy=ndx nob nom=ndy nob nth=nom 2 nfu=nth 2 ntr=nfu 2 not=ntr 2 nco=not 2 nh1=nco 2 nh2=nh1 2 nh3=nh2 2 nh4=nh3 2 nnn=nh4 2 start 4
As we may see, the magic of the original table declaration/setup is gone, giving room for clarity. A year later, the game had gone through a number of attempts to refactor and rearrange the code, resulting in a more distinctive separation of the various parts. Here, the declarative part assigning the labels for the property-"slots" is moved to a single block at the very end of the source, while the setup part is now rather using these labels than calculating the same addresses algorithmically in parallel.
Pace
In case you noticed the difference in the value assigned to the total instruction count in \mtc, this was compensating the higher speed of the positional calculation routines. Version 4 was all about MIT's PDP-1 having been upgraded to include the hardware multiply/divide option, which obviously resulted in a speedup of about a quarter of the total time spent in the calculations.
We might observe that this wasn't used to increase the pace of the game, rather the game was throttled to match the original implementation, the pace of it obviously considered to be just right. This shouldn't take much wonder, since this game was the first of its breed and there wasn't anybody who would have been used to this kind of interaction and the kind of eye-hand coordination required, not to mention having grown up with it. With everyone being a beginner, the game was considered to be "fast paced" already and an increased execution speed would have probably pushed it over the limits set by the motor skills and reaction abilities of most of the players. Cf. Steve Russell quoted in Brand, Stewart, "Spacewar — Fanatic Life and Symbolic Death Among the Computer Bums" (Rolling Stone, Sept 1972): "It's relatively fast-paced, [...] Thought does help you, and there are some tactical considerations, but just fast reflexes also help."
Moreover, there would have been other means to speedup the game, namely by adjusting the constants for linear and angular accelerations, or torpedo speed. But these had been carefully adjusted to provide the proper experience and to match the average skills of the players. Steve Russell (as quoted in the Rolling Stone article) again: "It was quite interesting to fiddle with the parameters, which of course I had to do to get it to be a really good game. By changing the parameters you could change it anywhere from essentially just random, where it was pure luck, to something where skill and experience counted above everything else. The normal choice is somewhere between those two."
(We may experience Spacewar! 3.1 to be a bit faster paced than version 2b. But this impression isn't due to the handling of objects and spaceships itselves, but is — as we'll see later — rather caused by a faster velocity of the torpedoes. However, we may conclude from this that either the pace of version 2b would have been experienced to be somewhat unsatisfactory, giving rise to the introduction of the parameters tabel in order to find the proper constants, or that the improving skills of the trained players would now have allowed for a speedier setup. Provided that there was nearly half a year between these two releases of Spacewar!, which would be quite some time to go with an unsatisfactory solution, I would rather vote for the second option, reflecting the increasing training and mastership in realtime gaming.)
That's all for now, stay tuned ...
Vienna, June 2014
www.masswerk.at
In case you would have found any errors or inconsistencies, or would have additional information,
please contact me.
*****
P.S.: It should be mentioned that there's always the possibility of some parts of this code being tributed by any of the other members of the Hingham Institute Study Group on Space Warfare, especially by Bob Saunders, who was lending a helping hand, where ever needed. While we may be quite sure about the main logic being by Steve Russell, it might be still unfair to forget the others in this context.
*****
◀ Previous: Intermission — Digging up the Minskytron Hyperspace
▶ Next: Part 4: The Outline Compiler
▲ Back to the index.